Interpreter für Mathematische Ausdrücke Wenn sich eine Berechnungsformel öfter für eine Anwendung ändert, hat man 2 Möglichkeiten: Source suchen, Formel ändern, dem Ganzen einen neuen Namen geben, Kompilieren, Verwirrung beim Benutzer erzeugen. Oder: Einen Interpreter für den Mathematischen Ausdruck schreiben, den Benutzer die Formel in eine Textbox eintragen lassen, Freude erzeugen.
Autor:  Dietmar G. Beyer	Bewertung:     [ Jetzt bewerten ]	Views:  23.972

Geben Sie hier Ihre persönliche Bewertung ab! Anzahl Bewertungen bisher: 4 Bewertung insgesamt: sehr gut Durchschnittliche Bewertung: 4.5 von 5 Sternen

sehr gut     gut     nützlich     mittelmäßig     mangelhaft

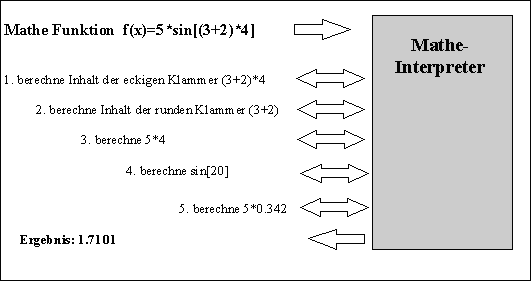
Wenn sich eine Berechnungsformel öfter für eine Anwendung ändert, hat man 2 Möglichkeiten: Source suchen, Formel ändern, dem Ganzen einen neuen Namen geben, Kompilieren, Verwirrung beim Benutzer erzeugen. Oder: Einen Interpreter für den Mathematischen Ausdruck schreiben, den Benutzer die Formel in eine Textbox eintragen lassen, Freude erzeugen.

Was müssen wir alles berücksichtigen?

• Fehlerhafte Formeln
• Doppelte Operatoren (-- ist =+, +-ist -)
• Division durch 0 geht nicht
• Punktrechnung geht vor Strichrechnung
• Klammer-Ebenen

Es soll ja eine natürliche Eingabe möglich sein, nicht das etwas seltsame Verfahren der umgekehrten polnischen Notation (die C++ Leute werden mich jetzt schlagen).

Die Formel soll dann lauten: Ergebnis (auch f(x) genannt)= x^2+(6x+5)*2-sin(x). Jede andere Formel soll so auch interpretiert werden können. Eine Kleinigkeit ist jetzt noch zu machen: Die Klammer bei sin(x) ist zwar eine Klammer, hat aber eine andere Bedeutung. Sie stellt den zu berechnenden Wert für Sinus (Cos, Tan ...) dar. Also einigen wir uns darauf, dass diese Klammer nicht rund, sondern eckig ‚[ ]’sein muss. Also sieht die Formel nun so aus: Ergebnis = x^2+(6x+5)*2-sin[x].

Wie soll das nun funktionieren? Eigentlich ganz einfach, wir bilden einfach nach, was wir in der Schule so gelernt haben (meine alten Mathe-Lehrer wären stolz auf mich). Einfach bei Klammern von innen nach außen lösen, Teil-Ergebnis einsetzen, Teile berechnen, Ergebnis einsetzen, .......

Ein wesentliches Merkmal des Interpreters ist die Rekursion. Wie funktioniert Rekursion? Dabei ruft sich die Funktion selbst wieder auf, um Teilergebnisse zu erhalten:

Einige Vorarbeiten sind als erstes zu machen:

Als erstes normieren wir die Formel, dass sie immer gleich behandelt werden kann und die gleichen Ausdrücke verwendet. Damit ist alles in kleinen Buchstaben und wir haben keinen Ärger mit Sin, sIn, SIN ….. Auch die Eingabe von Kommas als Dezimalzeichen, die Ärger machen könnten, sind nun computergerechte Punkte.

Function Norm(Text As String) As String
  ' alles klein
  Text = LCase(Text)
 
  ' alle Kommas zu Punkten machen
  Text = Replace(Text, ",", ".")
 
  ' keine Spaces
  Text = Replace(Text, " ", "")
  Norm = Entferne_PlusMinus(Text)
End Function

Oben haben wir schon das Problem mit Doppel-Operatoren gesehen, also lösen wir es.

Da die Kreativität des Menschen bei der Eingabe fast unbegrenzt ist, das trifft nicht nur die DAU’s, müssen die drei Fälle gelöst werden ++, +-, -+, und --. Doppel-Operatoren können auch nach dem Einsetzen von Teilergebnissen auftreten.

Und wie geht’s?
Wir suchen den Platz, an dem z.B. "--" steht, und ersetzen es dort mit dem (für uns) mathematisch korrekten +. Da so was in einer Formel mehr als einmal vorkommen kann, wird nach der Ersetzung eine Rekursion aufgerufen.

Function Entferne_PlusMinus(ByVal Formel As String) As String
  Dim Platz As Integer
  Dim NewFormel As String
 
  Entferne_PlusMinus = Formel
 
  If InStr(Formel, "++") Then Formel = Replace(Formel, "++", "+")
  If InStr(Formel, "+-") Then Formel = Replace(Formel, "+-", "-")
  If InStr(Formel, "-+") Then Formel = Replace(Formel, "-+", "-")
  If InStr(Formel, "--") Then Formel = Replace(Formel, "--", "+")
 
  Entferne_PlusMinus = Formel  
End Function

Da uns immer mal wieder in Teilergebnissen Kommas statt Punkten begegnen, ersetzt die Funktion RP die Kommas mit Punkten.

Function RP(Text As String) As String
  ' alle Kommas zu Punkten machen
  RP = Replace(Text, ",", ".")
End Function

Die Vorbereitungen sind abgeschlossen.

Arithmetischen Operationen

Jetzt versuchen wir uns an den arithmetischen Operationen als Beispiel für die Interpretation. Das Ergebnis soll formatiert mit 4 Nachkommastellen im String stehen.

Formel ist der zu interpretierende Ausdruck

Das ist der prinzipielle Vorgang am Beispiel der Multiplikation:
(Im Source sind die Operationen für Multiplikation, Division, Potenzierung, Addition und Subtraktion zu einer Funktion „MDHAS“ zusammengefasst)

Function MDHPM(ByVal Formel As String, Operator As String) As String
  ' Stelle an der das Zeichen gefunden wurde : hier ein * oder /
  Dim Platz As Integer
  ' Variable zu Vorwärts/Rückwärtslaufen im String
  Dim X As Integer
  ' Zähler
  Dim Y As Integer
  ' Welche Zahl steht vor dem Zeichen ?
  Dim vorne As String
  ' Welche Zahl steht nach dem Zeichen ?
  Dim hinten As String
  ' Neue Formel nach einer Teil-Lösung
  Dim NewFormel As String
  ' Speichern des alten Strings
  Dim AltStr As String
  ' Die jeweils anderen Operatoren
  Dim AlleOperatoren As String
  Dim gefunden As Boolean
  Dim i As Integer
  Dim NotFund As Boolean
  Dim AltStr_Hinten As String
 
  AlleOperatoren = "+-*/^"
 
  ' Erst mal sicherstellen, dass keine Doppel-Operatoren da sind.
  Formel = Norm(Formel)
  If InStr(Formel, "e") Then Exit Function  ' wegen 2.0000056e-3
 
  ' Für den Fall, dass keine Operation angefordert ist 
  MDHPM = Formel
 
  If FindOperator(Mid(Formel, 2), AlleOperatoren) = 0 Then
    MDHPM = Formel
    Exit Function
  End If  
 
  ' wo seht der Operator
  Platz = InStr(1, Formel, Operator)
  If Platz > 0 Then
    Y = 0
    X = Platz
    ' wandere zurück, um die Zahl vor dem Operator zu finden
    Do
      Y = Y + 1
      X = X - 1
      If X = 0 Then
        ' für den Fall, dass wir am Anfang gelandet sind
        vorne = Mid(Formel, X + 1, Y - 1)
        Exit Do
      End If
 
      If FindOperator(Mid(Formel, X, 1), AlleOperatoren) > 0 Then
        If Y = 1 Then        
          If InStr(Mid(Formel, X, 1), "+") Then
            ' nötig wg. -22*+12
            vorne = Mid(Formel, X, Y)
            Exit Do
          End If
          If InStr(Mid(Formel, X, 1), "-") Then
            ' nötig wg. -22*+12
            vorne = Mid(Formel, X, Y)
            Exit Do
          End If
        End If
        vorne = Mid(Formel, X + 1, Y)
        Exit Do
      End If         
    Loop
    AltStr = Left(Formel, X)
 
    ' Nun das Ganze vorwärts:
    Y = 0
    X = Platz + 1
    Do
      Y = Y + 1
      ' X = X + 1
 
      If Y > Len(Formel) Then
        hinten = Mid(Formel, X)
        AltStr_Hinten = ""
        Exit Do
      End If
 
      If FindOperator(Mid(Formel, X, 1), AlleOperatoren) > 0 Then
        ' (InStr(Mid(Formel, X, 1), AlleOperatoren) > 0 Then
        hinten = Mid(Formel, X, Y)
        AltStr_Hinten = Mid(Formel, X + Y)
        Exit Do
      End If          
    Loop
 
    ' Das wiederum so lange machen, bis wir die Zahl hinter
    ' dem Operator gefunden haben, oder das Ende erreicht ist.
    ' So wird jetzt unsere neue Formel berechnet ausschauen:
 
    If AltStr = "-" Then
      AltStr = ""
      vorne = "-" + vorne
    End If
    If AltStr = "+" Then
      AltStr = ""
      vorne = "+" + vorne
    End If
 
    Select Case Operator
      Case "*"
        NewFormel = AltStr & CStr((Val(vorne) * Val(hinten))) & AltStr_Hinten
        If InStr(1, NewFormel, "*") > 0 Then
          ' Die Rekursion aufrufen, da noch weitere Multiplikation zu machen sind
          NewFormel = MDHPM(NewFormel, Operator)
        End If
 
      Case "/"
        NewFormel = AltStr & CStr((Val(vorne) / Val(hinten))) & AltStr_Hinten
        If Err.Number = 11 Then
          ' Division durch 0 ist nicht möglich
          MDHPM = "unmöglich"
          Exit Function
        End If
 
        If InStr(1, NewFormel, "/") > 0 Then
          ' Die Rekursion aufrufen, da noch weitere Divisionen zu machen sind
          NewFormel = MDHPM(NewFormel, Operator)
        End If
 
      Case "^"
        NewFormel = AltStr & CStr((Val(vorne) ^ Val(hinten))) & AltStr_Hinten
        If InStr(1, NewFormel, "^") > 0 Then
          ' Die Rekursion aufrufen, da noch weitere Potenzierungen zu machen sind
          NewFormel = MDHPM(NewFormel, Operator)
        End If
 
      Case "+"
        NewFormel = AltStr & CStr((Val(vorne) + Val(hinten))) & AltStr_Hinten
        If InStr(1, NewFormel, "+") > 0 Then
          ' Die Rekursion aufrufen, da noch weitere Additionen zu machen sind
          NewFormel = MDHPM(NewFormel, Operator)
        End If
 
      Case "-"
        NewFormel = AltStr & CStr((Val(vorne) - Val(hinten))) & AltStr_Hinten
        If InStr(1, NewFormel, "-") > 0 Then
          ' Die Rekursion aufrufen, da noch weitere Subtraktionen zu machen sind
          NewFormel = MDHPM(NewFormel, Operator)
        End If
 
    End Select
    ' und fertig
    MDHPM = CStr(NewFormel)
    MDHPM = RP(Format(Replace(NewFormel, ".", ","), "0.0000"))    
  End If
End Function

Jetzt können wir Multiplizieren. Das Addieren und Subtrahieren geht genau auf die gleiche Art.

Interpreter für die vier Grundrechenarten

Beim Dividieren haben wir eine Falle zu beachten, die uns die Division durch 0 stellt. Da das nun mal nicht geht, muss dann eine Fehlermeldung her.

......
  Case "/"
    NewFormel = AltStr & CStr(CDbl(Val(vorne) / Val(hinten))) & Mid(Formel, X)
    ' Division durch 0 ist nicht möglich
    If Err.Number = 11 Then
      MDHPM = "unmöglich"
      Exit Function
    End If
......

Vom Prinzip her sind nun die vier Grundrechenarten verfügbar und wir könnten eine aufrufende Funktion schreiben:

Public Function Mathe_Interpreter(ByVal Formel As String) As String
  Formel = Norm(Formel)
 
  ' Berechne und entferne cos[ ],sin[ ],tan[ ]und atn[ ]
  If InStr(1, Formel, "[") > 0 Then Formel = CSTA(Formel)
 
  ' Berechne den Klammerinhalt und entferne die Klammer
  If InStr(1, Formel, "(") > 0 Then Formel = Klammer(Formel)
 
  ' Berechne und entferne ^
  If InStr(1, Formel, "^") > 0 Then Formel = MDHPM(Formel, "^")
  ' Berechne und entferne *
  If InStr(1, Formel, "*") > 0 Then Formel = MDHPM(Formel, "*")
  ' Berechne und entferne /
  If InStr(1, Formel, "/") > 0 Then Formel = MDHPM(Formel, "/")
  If Formel = "unmöglich" Then
    ' Bei Division Durch 0
    ' Fehler erzeugen
    Err.Raise 11
    Exit Function
  End If
  ' Berechne und entferne +
  If InStr(1, Formel, "+") > 0 Then Formel = MDHPM(Formel, "+")
  ' Berechne und entferne -
  If InStr(2, Formel, "-") > 0 Then Formel = MDHPM(Formel, "-")
  Formel = Norm(Formel)
 
  ' Und fertig !
  Mathe_Interpreter = Formel
End Function

Die Reihenfolge ergibt sich aus der Regel Punktrechnung geht vor Strichrechnung. Gut und schön, das funktioniert! Aber manchmal muss man doch Klammern setzen, um „5-2*3“ als „(5-2)*3“ zu beschreiben. Ist ja ein Unterschied ob das Ergebnis -1 oder 9 ist.

Die Art, die Formel zu durchsuchen, kennen wir ja schon, passen wir die Sache einfach an:

Function Klammer(ByVal Formel As String) As String
  Dim Platz As Integer
  Dim Y As Integer
  Dim X As Integer
  Dim VorneStr As String
  ' der ist neu, da das zu berechnende Teil 
  ' zwischen 2 Klammern steht
  Dim MittelStr As String
  Dim NeuFormel As String
 
  ' Die Doppelten wieder weg
  Formel = Norm(Formel)
 
  ' aus Sicherheit, wenn es keine Klammer gibt
  Klammer = Formel
  Platz = InStr(1, Formel, ")")
  If Platz > 0 Then
    Y = 0
    X = Platz
    Do
      ' das Innere der Klammer suchen
      Y = Y + 1
      X = X - 1
      If X = 0 Then Exit Do
      If Mid(Formel, X, 1) <> "(" Then
        MittelStr = Mid(Formel, X, Y)
      End If
    Loop Until Mid(Formel, X, 1) = "("
    VorneStr = ""
    If X > 0 Then VorneStr = Mid(Formel, 1, X - 1)
    ' die Hauptfunktion rekursiv aufrufen damit der innere Teil 
    ' der Funktion interpretiert wird
    NeuFormel = VorneStr & Mathe_Interpreter(MittelStr) & Mid(Formel, Platz + 1)
 
    If InStr(1, Formel, ")") > 0 Then
      ' Wieder in die Rekursion für mehr Klammern
      NeuFormel = Klammer(NeuFormel)
    End If
    Klammer = RP(Format(NeuFormel, "0,0000"))
  End If
End Function

Hier haben wir ein schönes Beispiel für die Rekursion, da in dem Ausdruck NewFormel = BeforeStr & Mathe_Interpreter (MiddleStr) & Mid(Formel, Platz + 1) unsere Hauptfunktion aufgefordert wird, den Klammerinhalt zu berechnen. So wird der Klammer-Salat langsam von innen nach außen, wie es sich gehört,aufgelöst.

Nun kann man es schon besser gebrauchen.

Trigonometrischen Funktionen

Die einfachen trigonometrischen Funktionen cos, sin, tan, und atn (Arcus-Tangens, da war doch was? ), kurz CSTA, haben wir am Anfang schon als einen Sonderfall gesehen. Da müssen die Klammern anders aussehen. Sie müssen in eckigen Klammern stehen. Nur so können wir mit vertretbarem Aufwand sicher das Argument in der Klammer identifizieren.

Public Function CSTA(ByVal Formel As String) As String
  Dim Platz As Integer
  Dim Y As Integer
  Dim X As Integer
  Dim VorneStr As String
  Dim MittelStr As String
  Dim NeuFormel As String
  Dim XType As String
 
  Formel = Norm(Formel)
  CSTA = Formel
  Platz = InStr(1, Formel, "]")
  If Platz > 0 Then
    Y = 0
    X = Platz
    Do
      ' suche das Innere der Klammer
      Y = Y + 1
      X = X - 1
      If X = 0 Then Exit Do '
      If Mid(Formel, X, 1) <> "[" Then
        MittelStr = Mid(Formel, X, Y)
      End If
    Loop Until Mid(Formel, X, 1) = "["
    VorneStr = "" '
    If X > 0 Then VorneStr = Mid(Formel, 1, X - 4)
    If X > 0 Then XType = Mid(Formel, X - 3, 3)
 
    Select Case XType
      Case "cos"
        NeuFormel = VorneStr & CStr(Cos(Format(MittelStr, "0.0000"))) & _
         Mid(Formel, Platz + 1)
      Case "sin"
        NeuFormel = VorneStr & CStr(Sin(Format(MittelStr, "0.0000"))) & _
          Mid(Formel, Platz + 1)
      Case "tan"
        NeuFormel = VorneStr & CStr(Tan(Format(MittelStr, "0.0000"))) & _
          Mid(Formel, Platz + 1)
      Case "atn"
        NeuFormel = VorneStr & CStr(Atn(Format(MittelStr, "0.0000"))) & _
          Mid(Formel, Platz + 1)
    End Select
 
    If InStr(1, NeuFormel, "]") > 0 Then
      ' und ab in die Rekursion
      NeuFormel = CSTA(NeuFormel)
    End If
    CSTA = RP(Format(NeuFormel, "0.0000"))
  End If
End Function

Wie man die übrigen trigonometrischen Funktionen berechnet hab ich mal im Anhang zusammengefasst. Wer will, kann sie ja einbauen.

Sonstige mathematische Funktionen

Wurzelziehen:
Kann man wie die Multiplikation implementieren, muss aber darauf achten (siehe Division), dass das Argument nicht 0 oder kleiner ist.

Logarithmen:
Wer die Beschreibung der Log Funktion aufmerksam liest, der wird feststellen, das damit eigentlich mathematisch LN, der Logarithmus zu Basis e (Euler-Zahl , wie Pi eine unendliche Zahl, ungefähr 2,718282) gemeint ist.
Der Zusammenhang zwischen Logarithmen zur Basis e und Logarithmen zur Basis 10, die, mit denen wir in der Schule zu tun hatten ist:

Static Function Log10(X as dbl) as dbl
   Log10 = Log(X) / Log(10#)
End Function

oder allgemeiner für eine beliebige Basis

Static Function LogB(X as dbl, Basis as dbl) as dbl
   Logb = Log(X) / Log(Basis)
End Function

Die Exp-Funktion stellt die Umkehrfunktion zur Log-Funktion dar und wird manchmal als Anti-Logarithmus bezeichnet.

Bei der Implementation ist darauf zu achten, dass der Wert > 709,782712893 einen Fehler verursacht.

Rundungs-Funktionen:
    ABS(), FIX() , INT() und SGN(), kurz AFIS
    Werden wie Cos(), Sin(), Tan() und Atn() implementiert.

Nun die entscheidende Frage: Wie rufe ich das auf? Was fange ich damit an? Wo ist der Nährwert?

Aufruf mit

On Error Resume Next
Dim X As Double 
X = Mathe_Interpreter ("2+3*4^2*2*cos[3]+2") 
If Err.Number = 11 Then MsgBox "Division durch 0", , "nicht lösbar"
If Err.Number = vbObjectError + 555 Then 
  MsgBox "Formel Struktur nicht erlaubt oder fehlerhaft", , "Fehlerhafte Gleichung" 
End if
On error goto 0

Weitergehen ist dann möglich bei einer Formel
Formel = „x^2+(6x+5)*2-sin[x]“

Dim i as long
Dim X as dbl
On Error Resume Next
 
For i=1 to 22
  X= Mathe_Interpreter (replace(Formel, x, cstr(i)))
 If Err.Number = 11 Then MsgBox "Division durch 0", , "nicht lösbar"
 If Err.Number = vbObjectError + 555 Then 
   MsgBox "Formel Struktur nicht erlaubt oder fehlerhaft", , "Fehlerhafte Gleichung" 
 End if
Next
On error goto 0

Anhang

Abgeleitete trigonometrische Funktionen: